
This is an overview of foundational topics in mathematics, originally intended for Sophie (who can ignore topics marked with “*” for now if she wants!).
Here are the main ones:
| Operator | Name | Example |
|---|---|---|
| + | Plus, addition | 1 + 2 = 3 |
| - | Minus, subtraction | 8 - 3 = 5 |
| × or * | Times, multiplication | 2 × 5 = 10 |
| – you can also leave out the “×” | 3z = 3 × z | |
| / or ÷ | Divided by, division | 15 / 5 = 3 |
| – normally division gives a single value | 14 / 5 = 2.8 = 2 4/5 (two and four fifths) | |
| – but you can also have a quotient and remainder | 14 / 5 = 2 remainder 4 | |
| mod | Mod, modulus: the remainder after division | 14 mod 5 = 4 |
Some operators are just used on a single number:
| Operator | Name | Example |
|---|---|---|
| - | Unary minus, negation | -(2 + 3) = -5 |
| ! | Factorial: multiply all the numbers from one up to the number | 3! = 1 × 2 × 3 = 6 |
There are some other common operations too:
| Symbol | Name | Example |
|---|---|---|
| | n | | Absolute value: make n into a positive number | | -3 | = 3 |
| √n | Square root: the number that multiplied by itself equals n | √16 = 4 |
| nm or n ^ m | n to the power of m: multiply n by itself m times | 23 = 2 × 2 × 2 = 8 |
An expression is a “mathematical sentence” like 1 + 2 or 3 × 4, or or even just a single number like 23. Evaluating an expression means working out its value.
The order of operations tells you which operations to do first. The main thing to remember is that addition and subtraction come last. Parentheses (also called brackets) can be used to group things too.
Powers and factorials get evaluated first:
The same kind of thing happens with division:

Multiplying by a negative number reverses the direction along the number line. For example, -2 × 3 = (left by two) three times = -6:

Multiplying two negative numbers, such as -2 × -3, reverses the direction twice – so the result is positive:

The same thing applies to division. So:
In the expression “n mod m”, m is called the modulus. Adding the modulus to n doesn’t change the value of n mod m. For example:
The symbol “≡” means “is equivalent to.” So you could say:
A familiar example is 24 hour time, which has hours from 0 to 23 then repeats from 0 again. You can use mod to work out what time it will be a certain number of hours from now:
If the power is 2 or 3, people usually say squared or cubed respectively. For example, 52 is “five squared”
Somewhere in history someone noticed that na × nb = na+b. Which is obvious if you write out an example:
Using that formula you can work out what happens if the power is not a positive integer. It turns out that:
Some examples:
Another useful formula is:
For example:
As another example, if you square the square root of something, you get the original number again:
The nth root of m is written as n√ m. For n = 3 this is called the cube root, 3√m.
The power of a fraction involves nth roots. The formula is:
When m/n = 1/2, this just becomes the square root:
A more complex example is:
But if the power is a fraction a/b, then na/b only makes sense if b is an odd number:
| Symbol | Name |
|---|---|
| < | Less than |
| > | Greater than |
| ≤ or <= | Less than or equal |
| ≥ or >= | Greater than or equal |
| ≠ or <> | Not equal |
| ≈ | Approximately equal (e.g. √2 ≈ 1.414) |
Two < or <= comparisons can be combined together to make a range of values. For example:
The word inclusive is used when both comparisons are <=, such as 10 <= x <= 20 (x is between 10 and 20 inclusive).

Intervals are written using two different kinds of parentheses, ( ) and [ ]:
Intervals can also be infinite, represented using the infinity symbol ∞. For example (0, ∞) is the same as x > 0.
Or it can come in the middle a list, meaning “fill in the mising values”:
You can read this as “the sum of all values of n for n = 1 up to n = 10”, which can be written as:
Another example is:
which is the sum of all values of n2 from 1 to 4:
A rational number is a number that can be written as a fraction (“rational” means it is a ratio of two other numbers). For example, 2/3 (two thirds) or 1 3/4 (one and three quarters). All integers are also rational numbers.
A real number is any number, which includes things like √2 and pi which are infinitely long without repeating. All integers and all rational numbers are also real numbers.
There is a special symbol for each type of number:
Fractions can be split into an integer part and a fractional part. For example, 22/7 = 3 1/7 (three and one seventh).
To find the reciprocal of a number, swap the numerator and the denominator (treat integers as having a denominator of 1):
If the numerator and denominator do not have a common divisor, the fraction is irreducible. 5/8 and 3/7 are both irreducible, but 4/6 is not, because it can be reduced to 2/3.
Two fractions can be multiplied together just by multiplying the numerators and denominators:
To divide one fraction by another, turn the second fraction upside down and then multiply them:
Some rational numbers are written as repeating (or recurring) decimals:
Irrational numbers do not have a repeating pattern:
You can round down, also called the floor function. So 3.0, 3.1 and 3.9 all become 3.
You can round up, also called the ceiling function. So 5.1, 5.9 and 6.0 all become 6.
You can also round to the nearest integer: round down if the fractional part is less than 0.5, or round up if it is greater than or equal to 0.5. So 7.3 becomes 7, 7.9 becomes 8 and 7.5 becomes 8.
If you need to write a number to fewer significant figures than it already has, round the last digit up or down to be as close as possible to the original. For example:
Significant figures are related to the precision of a value. It is important not to be overprecise with measurements. For example, you might say that a building is 25 metres tall, but saying it is 25.0001 metres is probably being too precise.
The precision of a value can also reflected by giving it a tolerance as ± (plus or minus) some amount. For example, you might estimate a distance as 15.3 km ± 100m (from 15.2 to 15.4 km), or a time as one hour ± 5 minutes (from 55 to 65 minutes).
It can also be written like this: 3.4E+12 or 3.4E12.
In the above examples, 3.4 is called the mantissa and 12 is the exponent. To find the value of the number, shift the decimal point to the right by the exponent if it is positive or to the left if the exponent is negative:
Think about what it really means when you write a number like 323. The first “3” obviously doesn’t mean the same as the last “3”. If you break it down into digits:
Our numbering system is called base 10 because each digit is multiplied by a power of 10 (remember that 100 equals 1):
But 10 isn’t the only possible base. Two other bases commonly used in computing are binary (base 2) and hexadecimal (base 16).
Here is an algorithm for converting a positive integer into a binary number (which gets written backwards):
If you try it with 18, you should get 01001, which when reversed gives the answer: 10010.
There is a relationship between binary and hexadecimal numbers. Since 24 = 16, one hexedecimal digit corresponds to four binary digits, which makes it easy to convert between them: just break the binary number into groups of four, then convert each group individually.
Finding the factors of a number is called factorising or factorisation.
A prime number is a number whose only factors are 1 and itself. The first few prime numbers are: 2, 3, 5, 7 and 11. (The number 1 is not counted as prime).
Every positive integer can be written as the product (multiple) of powers of its prime factors. For example, the prime factors of 12 are 2 and 3; 12 = 22 × 3. Here are some more:
Formulas contain variables which you need to assign a value and sometimes constants with a fixed value. For example, the area of a circle is:
where r is a variable (the radius of the circle) and π is a constant (approximately 3.1415926).
Evaluating a formula involves substituting (“plugging in”) the values of the variables and constants then calculating the result. If the radius is 10 then the area of the circle = π × 102 ≈ 314.16.
It is important to keep track of the units you are using. For the area of a circle, if the radius is in metres (m) then the result will be in square metres (m2); but if the radius is in inches or centimetres, then the result will be in square inches or square centimetres.
Here are some common formulas:
This is similar to the formulas from the previous section, but these ones are called equations. The idea is to find the value of all the variables, in this case x and y.
You can do so using one basic idea: whatever you do to the left hand side (the part before the “=”), do the same to the right hand side (after the “=”).
For example, if you take equation (2) and subtract y from both sides, you get a new equation (3):
(“∴” is pronounced “therefore”, and means that something follows logically from the thing above it).
Now we have two equations that both have the same left hand side, equations (1) and (3). That means their right hand sides are equal as well:
This is useful because now we have an equation that only has “y”s in it and no “x”s. If we rearrange equation (4) so that all the “y”s are on the left and everything else is on the right, we can find the value of y:
Now that we know the value of y, we can use either of the original equations (1) or (2) to find the value of x. We’ll use equation (1):
So the solution to the original set of equations is: x = 5 and y = 1.
You solve an inequality by getting the variable by itself on the left hand side:
There is an important thing to remember though. The direction of the < or > must be reversed if you multiply or divide by a negative number:
The same thing happens if you swap the left and right sides:
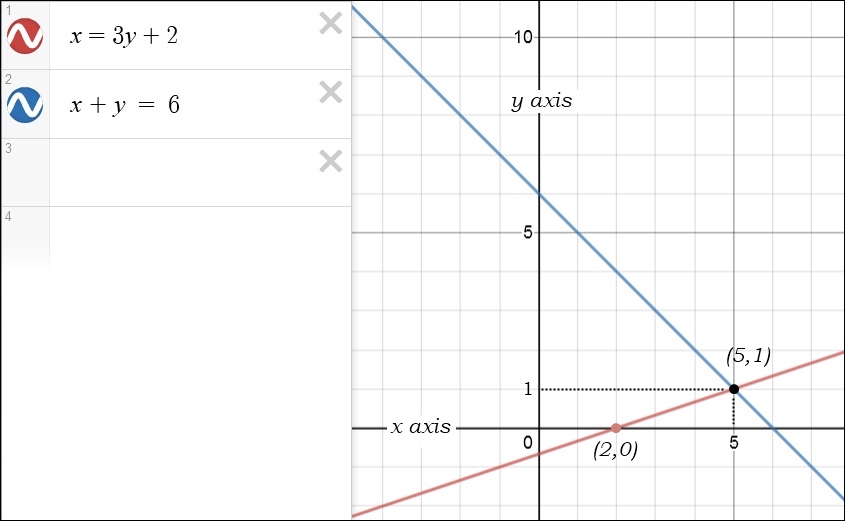
If you go to a website like www.desmos.com/calculator you can just type in some equations containing x and y and it will draw them for you:
The red line is for the equation x = 3y + 2 and the blue line is for x + y = 6.
The black horizontal line is called the x axis and the vertical line is the y axis. Every point on the graph has an x and y coordinate, written as: (x, y).
For example, the point where the red and blue lines meet has the coordinates (5, 1), which are the values we found when we solved these equations in the previous section: x = 5 and y = 1.
You can also use the graph to see where the lines intersect the x or y axis. For example, the red line intersects the x axis at (2, 0), i.e. at x = 2 and y = 0.
The general form of a linear equation is y = ax + b.
If b is 0 (so the equation is just y = ax) then x is proportional to y.
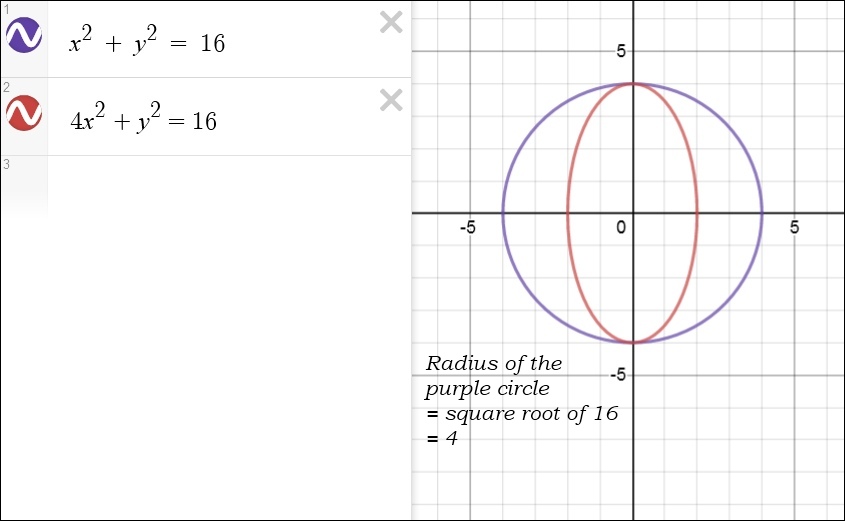
An equation with a (positive) x2 and y2 is drawn as a circle or ellipse:
If the equation is in the form y = a/x then x is inversely proportional to y.
Here are a few more graphs involving x3, 2x and | 2x | (the absolute value of 2x):
The a, b and c values are called coefficients; a cannot be 0.
To solve the equation and work out the value of x, you can use the quadratic formula:
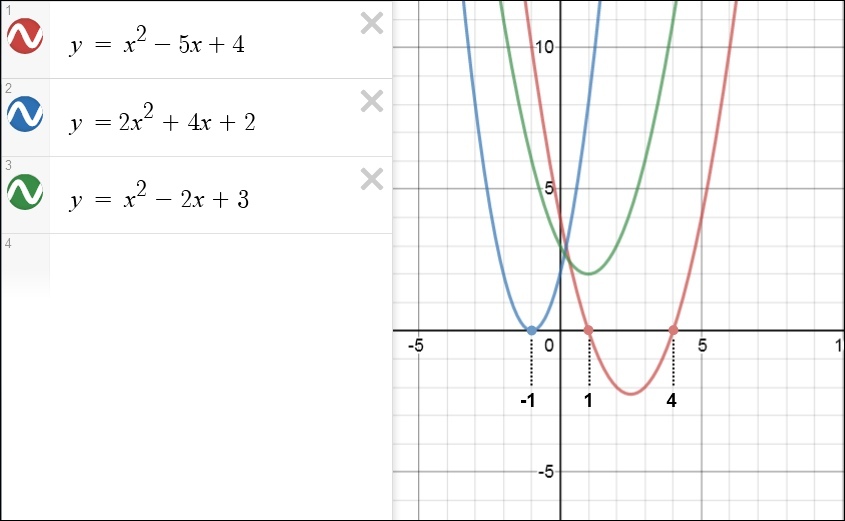
This can have 0, 1 or 2 solutions. For example:
You can verify these solutions by looking at the graph of each equation and finding the x value when y = 0 (that is, where they touch the horizontal x axis):
The number that goes with each term is called the coefficient. In the first example above, the coefficient of x3 is 1 and the coefficient of x is 3.
Adding, subtracting or multiplying two polynomials gives another polynomial:
Polynomials can often be factorised by breaking them into smaller polynomials multiplied together:
Functions are written in the form: name(parameter) = expression. The parameter is a variable such as x. For example:
Here the function name is f, the parameter is x and the expression is x2. You can use the function like this:
Functions can have more than one parameter:
So:
The values you use for the parameters are called the arguments to the function (6 and 2 in the above example).
For example, if f(x) = 2x then f-1(x) = x / 2.
A function and its inverse “cancel each other out”, which means that f(f-1(x)) always equals x.
You can define a sequence using a function, with f(0) (or sometimes f(1)) as the first value. So the sequence of positive integers can be defined as:
So p(0) = 1, p(1) = 2 and so on.
Sometimes sequences are written using subscripts instead of function form: p0 = 1, p1 = 2, ...
The Fibonacci sequence is an example of recursion. Each number in the sequence is the sum of the previous two numbers:
So that there is a starting point, we define the first two values explicitly:
Now we can calculate some of the other values:
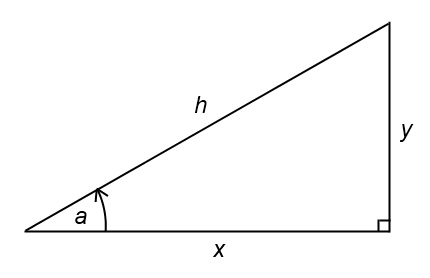
If you draw a right angled triangle like this:
with side lengths x, y and h (h stands for hypotenuse) and angle a at the bottom left, then:
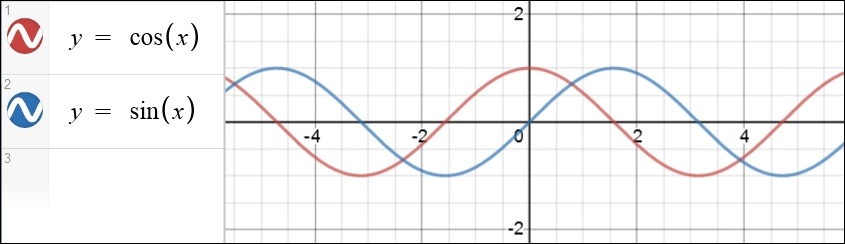
The graphs of these functions are periodic (they repeat forever):
Imagine someone is travelling from point A to point B at constant speed. The coordinates of A and B are (3, 14) and (9, 17) respectively. If it takes 30 minutes to go from A to B, what are their coordinates 10 minutes into the journey?
The parametric equations can be written as:
Now find values for a, b, c and d. We know the x and y values are (3, 14) at time 0 at the start of the journey and (9, 17) at time 30. So:
Now we can find b and d:
So the final parametric equations are:
Now we have a way to find the traveller’s coordinates at any time t. For t = 10:
So the coordinates are (5, 15).
The usual equation for a circle of radius r without using parameters is:
It turns out these parametric equations also create the same circle:
Since cos and sin are periodic (repeating) functions, t only needs a certain range of values: 0 <= t < 2π (since 2π is actually equivalent to 360°, and there are 360° in a circle).
You can use www.desmos.com/calculator to draw a parametric equation. Write it in the form “(x, y)” then fill in the range of values (write “pi” for π):
Try changing the x and y values and see what happens:
You could also try changing one of the numbers to a new parameter like u or v, then click on the “add slider” button that appears. This lets you easily experiment with variable values. (The range can be made into a parameter as well: change 2π to z).
Ellipsis and Sums
In a list of numbers, three dots “...” (called ellipsis) means “continue the same pattern.” The ellipsis can come at the end of a list, meaning “continue forever”:
Sums
The sum of a list of numbers can be written using the symbol Σ (Greek capital sigma), called sigma notation:
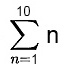
= 55
= 1 + 4 + 9 + 16
= 30Kinds of Numbers
An integer is a whole number, like 45 or -3 or 0.
Symbol
Name
Description
Examples
ℝ or R
Real
All numbers
√2, pi, 1/3, 5
ℚ or Q
Rational
Fractions (including whole numbers)
1/2, 7 3/4, 4
ℤ or Z
Integer
Whole numbers
-3, 0, 100
ℕ or N
Natural
Positive integers (as well as 0)
0, 1, 2, 50
Fractions
A fraction (or rational number) is equal to one integer divided by another, called the numerator and the denominator. For example:
* Simplifying Fractions
If the numerator and denominator have a common divisor (meaning they can both be evenly divided by the same number) then the fraction can be simplified by dividing them both by the greatest common divisor. For example, for the fraction 30/42, the highest number that 30 and 42 can both be evenly divided by is 6; 30/6 = 5 and 42/6 = 7; so 30/42 can be rewritten as 5/7.
* Operations on Fractions
Two fractions can only be added or subtracted if they have the same denominator. To make that happen, multiply the top and bottom (numerator and denominator) of the first fraction by the second fractions’s denominator and vice versa; then just add the numerators together.
= (2 × 7) / (3 × 7) + (5 × 3) / (7 × 3)
= 14/21 + 15/21
= 29/21
= (2 × 5) / (3 × 7)
= 10/21
= 2/3 × 7/5
= (2 × 7) / (3 × 5)
= 14/15Decimals and Rounding
Real numbers can be written in decimal form. For example:
Rounding Numbers
Numbers can be rounded to make them into integers. There are three different methods of rounding:
To n decimal places
You can round a number to a certain number of decimal places, which is similar to rounding to the nearest integer. For example:
* Significant Figures and Precision
Decimal numbers can be written to a certain number of significant figures, which is the number of digits in a row ignoring zeros at the beginning and end. For example, 12.45 has four significant figures; so do 0.003456 and 98710000.
12.34825 to 3 significant figures = 12.3 (rounding down to 3 from “34825”)
* Scientific Notation
Sometimes you might see a number written like: 3.4×1012. This is called Scientific Notation, Exponential Notation or Standard Form in Britain.
1.25×10-2 = 0.0125
* Bases Other Than Ten
= 3 × 100
+ 2 × 10
+ 3 × 1
= 3 × 102
+ 2 × 101
+ 3 × 100Binary: Base 2
For binary numbers, only two digits are used: 0 and 1. Here is an example number in binary:
= 1 × 23
+ 1 × 22
+ 0 × 21
+ 1 × 20
= 8 + 4 + 0 + 1
= 13
If the number is odd, write 1, otherwise write 0.
Divide the number by 2 (round down).
Repeat from the beginning.
Hexadecimal: Base 16
For hexadecimal numbers, some extra digits are needed. After 0 ... 9 comes A, B, C, D, E, F; the letter A means 10 and F means 15. Here are some example numbers:
= 1 × 161
+ 10 × 160
= 26
100 base 16
= 1 × 162
+ 0 × 161
+ 0 × 160
= 256
* Factors and Prime Numbers
The factors of a positive integer are all the numbers which it can be divided by evenly (i.e. there is no remainder after division). For example, 12 has factors: 1, 2, 3, 4, 6 and 12.
63 = 32 × 7
90 = 2 × 32 × 5
Formulas, Constants and Variables
A formula is a way to calculate the value of something, such as the area of a circle or conversion from Farenheit to Celcius.
Name
Formula
Variables
Area of a circle
area = πr2
Radius r
Circumference of a circle
circumference = 2πr
Radius r
Area of a rectangle
area = w × h
Width w, height h
Celcius to Fahrenheit
F = C × 9/5 + 32
Temperature C in Celcius
Fahrenheit to Celcius
C = (F - 32) × 5/9
Temperature F in Fahrenheit
Algebra and Solving Equations
Algebra involves using letters like x and y to represent numbers, as in:
Inequalities
An inequality is an equation that uses a comparison like “<” or “>”:
Graphing Equations
It can be useful to graph (draw) equations in order to get a better idea of what is going on.
Linear Equations
The two equations we drew above are called linear equations because their graph is a straight line. If an equation only involves simple “x”s and “y”s, it will always be a line.
Other Kinds of Equations
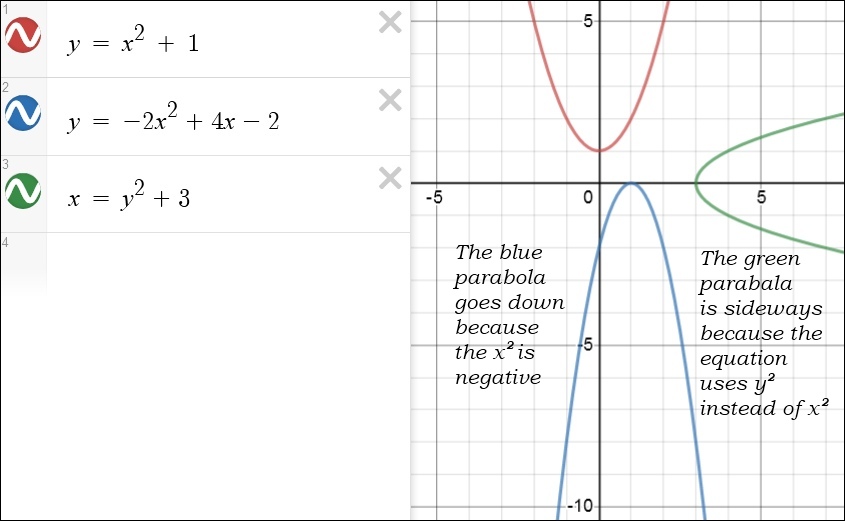
An equation involving x2 or y2 (but not both) is called a quadratic equation. Its shape is a parabola; here are three drawn on the same graph:
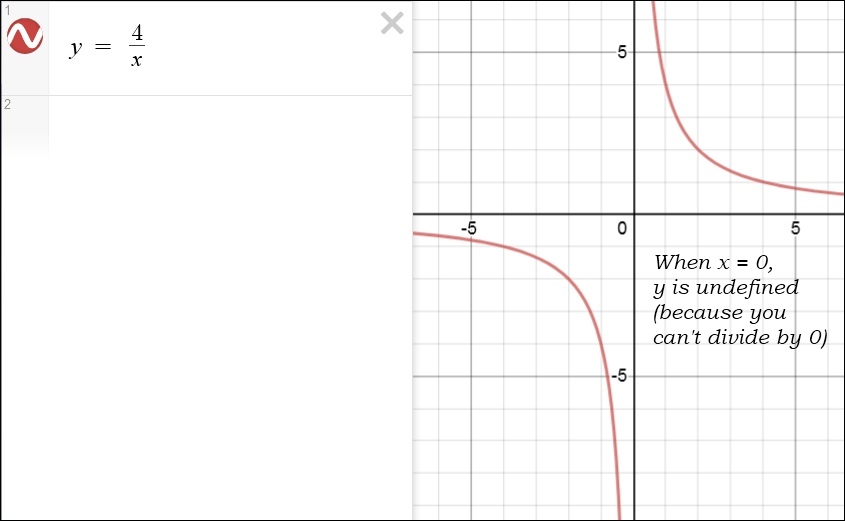
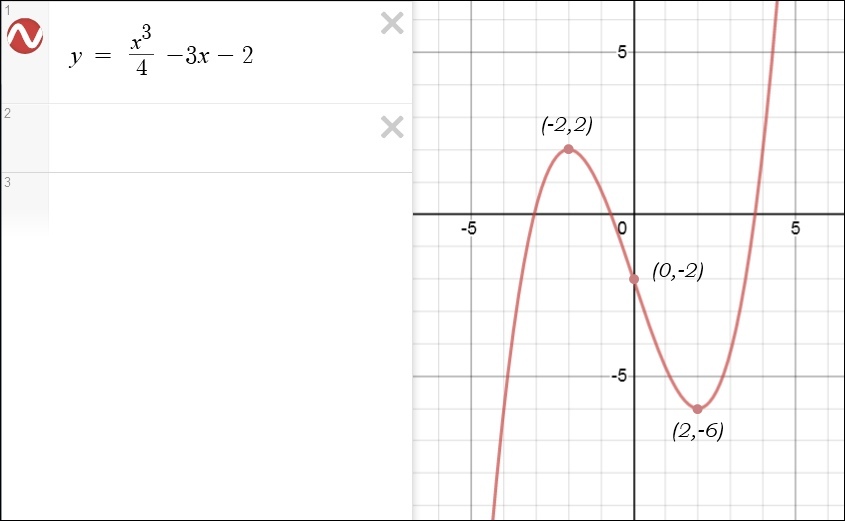
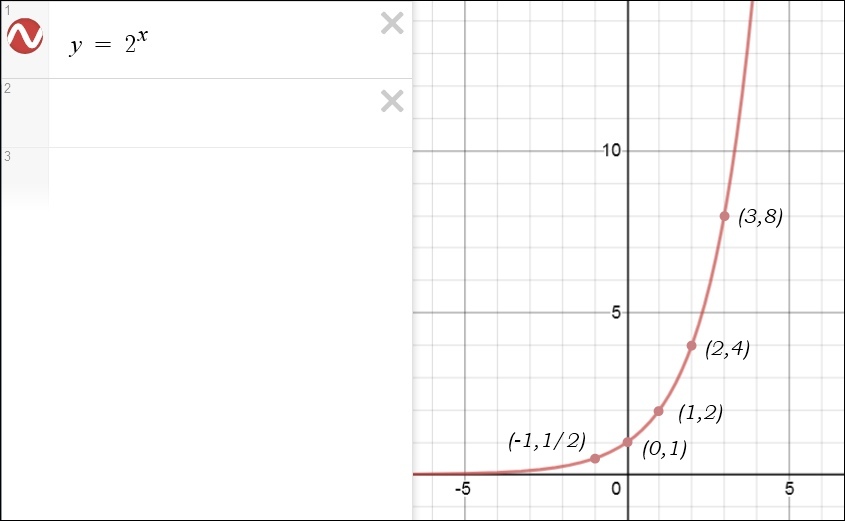
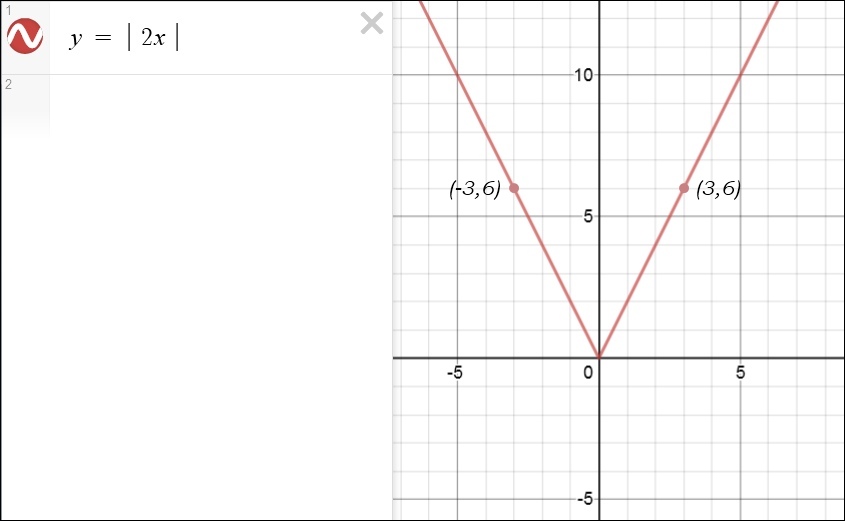
* Quadratic Equations
A quadratic equation looks like:

* Polynomials
A polynomial is an expression containing integer powers of a variable (or sometimes more than one variable). The powers cannot be negative. For example:
Functions
A function is something that takes a number, does something to it and gives you the result.
Inverse functions
The inverse of a function is its opposite. The inverse of f(x) can be written as f-1(x) (which is not the same thing as x to the power of -1).
Functions and sequences
A sequence is an infinitely long list of numbers, such as the positive integers: 1, 2, 3, ...
* Recursive functions
A function can be defined in terms of itself, which is called recursion.
* Trigonometry functions
Most calculators include buttons that say “sin”, “cos” and “tan”, short for sine, cosine and tangent. These are trigonometry functions.
* Parametric Equations
Parametric equations use an extra variable called a parameter to control the value. A typical parameter is t (for “time”).
Parametric equation of a circle

Maths –
Home
Questions or comments to:
[email protected]