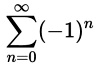
There is an interesting video on YouTube by Numberphile about this series:
The question is, what does it actually add up to?
If you bracket the terms as follows, the total is clearly 0:
But an alternative bracketing gives a total of 1:
Or you can use algebra instead:
There is a problem here!
If the running total for a sum comes from a fixed set of values (0 and 1), the overall sum must be one of those values. So how do you choose which one? In this case there is no way to choose, so the sum is indeterminate.
Some series diverge instead:
For the series 1 - 1 + 1 - 1 ... if you interpret “=” as meaning “the value that it gets closer and closer to,” then the answer is that it doesn’t; there is no such value.
This goes against the grain for a lot of people. We want there to be an answer! (As seen by the 15000+ comments on YouTube). But sometimes the question itself is the problem.
To arrive at the answers 0 and 1, the series was bracketed in two different ways:
For the first bracketing to be valid, the series must have an even number of terms. The second bracketing requires an odd number of terms. So is infinity even or odd?
A proof that the number of terms is even goes like this. Assign each term an index, starting from 1. Every odd index can be paired with an index one higher: (1 2), (3 4), (5, 6) and so on. Since it can be divided into pairs, there must be an even number of indexes/terms.
However, a similar argument can be made if you exclude the index 1. All of the even indexes can be paired with an odd index one higher: (2 3), (4 5), (6 7) etc. Since there is a single number (1) left over after pairing up the rest of the indexes, the number of indexes/terms must be odd.
(Similar arguments can be used to show that infinity is both divisible and not divisible by 3, 4 or any other integer >= 2).
The problem is that infinity cannot be treated like a normal number; you can’t assign it to be just even or odd (ignoring special types of infinity such as 2 or 3 to the power of another infinity, which must be even or odd respectively – but let’s not get into that).
Say you’re not convinced. You decide that infinity is even and the series should be seen as an infinite number of “(1 - 1)”s, so the sum is 0. That would mean that the running total 1, 0, 1, 0 ... ends on 0. Which is like saying, “If you start walking on your left foot and keep on walking forever, you must end on your right foot.” The symmetry of taking an equal number of steps with both feet might feel attractive, but it is really an arbitrary choice. (The illusion is that a choice must be made at all).
But the expression in [3] is not actually S (even though it looks identical at first glance), so step [4] is not valid.
Is it really possible to have two expressions that look the same but are not? Here’s another way to think about it. Say we weren’t dealing with an infinite series, just the first three terms. The equations become:
Clearly the expression in [C] is not equal to X; there is an extra -1 at the end.
Let’s try it with four terms:
This time there is an extra +1 at the end.
Depending on whether the number of terms is even or odd, there is always an extra +1 or -1 at the end of the series when you perform the “1 - (series)” operation. The same thing happens when the series is infinite: an extra term is being added.
The reason this isn’t immediately obvious is because the extra term is hidden in the “...” part at the end:
Why does this extra term matter if we are dealing with an infinite series anyway? Because we are treating the series as having a particular value; so adding or subtracting 1 from it changes that value. It is just as invalid to add 1 to it as to add 237 to it – either way, the value has changed.
If you take into account the extra +1 or -1, the proof becomes:
... which leads to S being equal to 0 if infinity is treated as even (value S+1) or 1 if it is treated as odd (value S-1). But as stated above, infinity can’t be assigned to be just odd or even, so the value is indeterminate.
Is there anything suspicious about this proof?
We just proved that summing all the powers of two from zero to infinity equals -1!
The error is on line [4]. The expression 1 + 2 + 4 + 8 + ... on the right hand side of line [3] does not actually equal A; it equals 2A + 1.
Series A and 2A both have the same number of terms, most of which are identical. If you align like terms by shifting 2A right one position, you can see that an extra term gets added “at the end” of 2A:
In other words, 2A is the same as A without the leading 1 plus an extra term equal to A + 1. So line [4] should really say:
Adding ones
What about a simpler series:
One way to spot this kind of this thing is to keep track of the number of terms. The number of “+1”s on line [3] is three more than the number of “+1”s in B, so they are not the same series.
Decreasing powers of two
Here is a case where messing with the terms in an infinite series works out OK:
Which is the correct result.
After excluding the leading 2, the infinite series 1 + 1/2 + 1/4 + 1/8 + ... on line [2] has one less term than C. But since the values are heading towards 0, the extra term makes no difference “at infinity”, so it is reasonable on line [3] to equate the series with C (in the limit).
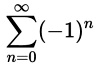
The formula for the sum to infinity of the series ark is a / (1 - r). Here a = 1 and r = -1, so the result is 1 / (1 + 1) = 1/2. But this isn’t valid either, because the formula only applies when the absolute value of r is less than one. So scratch that method.
Another approach is to find the Cesàro sum of the series: the limit of the partial sums. The partial sums are 1, 0, 1, 0, 1, 0 ... and the running average of these is 1/1, 1/2, 2/3, 2/4, 3/5, 3/6 ... which has a limit of 1/2.
But this is not surprising. Of course the average of all those 1s and 0s is 1/2! Averaging is a way of reducing a set of numbers to a single representative value; it doesn’t always give you “the” value of something. In the process of reduction to a single number, some information was lost: the fact that the running total oscillates between two different values, 0 and 1.
A way to visualise the sum 1 - 1 + 1 - 1 ... is to imagine someone with an empty bag, putting a stone into it then removing it again for all eternity.
Now try to formulate the appropriate question:
Well, there is no end, so that isn’t the right question. How about:
This is a good question for something that is either constant or is closing in on a particular value or increases/decreases forever, but none of those things are happening in this case. What about:
The answer to the first question is no, so there is no meaningful way to answer the second question.
Now don’t get me started on 1+2+3+ ... = -1/12!
Questions or comments to:
[email protected]