The Monty Haul problem

Maths – Home

Monty Haul was the host of Let’s Make a Deal, a TV show that inspired the following problem:

You are a contestant on a game show. There are three doors in front of you: one has a car behind it and two have goats. You must pick a single door; if it turns out to be the one with the car, you win the game.

However, after you choose a door, the host opens another one and reveals a goat (he knows where the car is so he can always do this; if both other doors have goats he picks one at random). He then asks if you want to change doors.

Should you switch or not?

The answer is yes: there is a 2/3 chance that by changing doors you will win the game, and just 1/3 if you stay with your original choice.

This can feel very counterinutive. Surely if there are two possibilities, there is a 50% chance of either one?

Here are a few different ways to look at the problem.

• (1) Decision tree
• (2) Roulette wheel
• Digression: The Monty Fall problem
• (3) Card game
• (4) Cups of water
• Digression: 100 doors
• (5) Two for the price of one
• (6) To shift or not to shift
• (7) Simulation
• Probability and intuition

(1) Decision tree

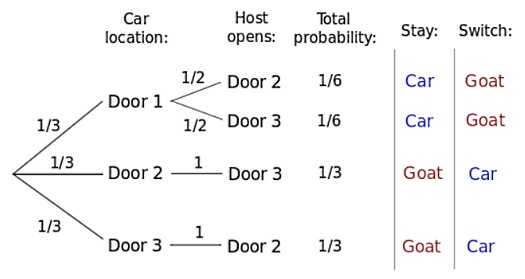
This diagram is from the Wikipedia entry. It assumes the contestant chose door number 1.

There are four possibilities, but they do not have the same probability:

• The car is behind door 1 (1/3). The host then picks another door at random:
  • Host opens door 2 (1/2). Total probability = 1/3 x 1/2 = 1/6.
  • Host opens door 3 (1/2). Total probability = 1/3 x 1/2 = 1/6.
• The car is behind door 2 (1/3). Host opens door 3. Total probability = 1/3.
• The car is behind door 3 (1/3). Host opens door 2. Total probability = 1/3.

In the first two cases, where the car is behind door 1, the contestant wins by staying; but the probability is only 1/6 + 1/6 = 1/3.

In the last two cases, where the car is not behind door 1, the contestant wins by switching. The probability is 1/3 + 1/3 = 2/3.

(2) Roulette wheel

Another way to visualise the problem space is to draw it as a kind of roulette wheel (from this page).

• The inner ring is the door the car is behind.
• The middle ring is the door chosen by the contestant.
• The outer ring is the door opened by the host.
• Red means the player wins by switching, blue by staying.
• There are 12 red and 6 blue spaces, making the probability of winning 12/18 = 2/3 if the contestant switches.

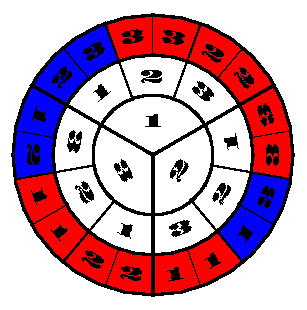
To paraphrase that page: when the car’s door is not chosen (which happens 2/3 of the time), the host effectively tells the contestant where the car is.

Digression: The Monty Fall problem

If the problem is altered so that the host picks a door at random (other than the contestant’s door), and if he accidentally reveals the car then it doesn’t count and they start again from scratch, the diagram changes:

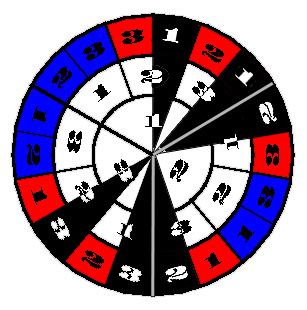
The “start again” states are marked in black. Now there are an equal number of red and blue sections (6 each), so the probability of winning by staying or switching becomes 1/2 in both cases.

This alternate version is sometimes called the Monty Fall problem: the host falls and accidentally opens a door at random.

Some things to notice:

• Only red sections have been blacked out.
• In the original version of the game, red sections come in pairs of the same number. This is because the player has not picked the car’s door (red means “switch to get the car”), leaving the host only one possible door to open without revealing the car.
• In the alternate version, red sections come in pairs of different numbers: one just like the original version, and one where the outer ring equals the inner ring (the host reveals the car). These are the sections that have been blacked out.
• The blue sections in the original and alternate version are identical. This is because blue means “stay”, so the player chose the car’s door, and the host never opens that door.

It may seem a little paradoxical that the Monty Hall and Monty Fall problems have different answers, since the actions look the same in both versions: the contestant chooses a door, then the host opens a door revealing a goat. But having 1/3 of the games cancelled makes a difference to the probabilites.

(3) Card game

Inspired by user “Schenck” on the Understanding the Monty Hall problem page:

• There are three cards in the game: an Ace, a King and a Queen. The aim is to have the Ace at the end.
• I pick a random card but do not look at it.
• Monty takes the other two cards and looks at them, then discards one (not an Ace).
• I can either keep my card, or swap it with Monty’s.

• When Bob looks at my card, what is the chance he sees an Ace?
• When Bob looks at Monty’s two cards, what is the chance he sees an Ace?
• Does the chance of Bob seeing an Ace in Monty’s hand change after he discards?

Another way to look at it: after Monty discards a non-Ace, the 2/3 probability that was previously distributed between his two cards now applies just to his remaining card.

If the idea of probabilities being redistributed sounds odd, read on.

(4) Cups of water

Imagine each door having a cup in front of it with an amount of water representing the probability of having the car. The cups start with 1/3 litre each.

Call the doors A, B and C. The contestant picks door A.

The host opens door B, revealing a goat. Now we know that the probability of door B having the car is 0, so we should empty out cup B – but where does the water go?

The critical thing to remember is that when the host decided which door to open, he was only choosing between doors B and C. Door A is not considered because of the rules of the game (he can’t open the door that the contestant chose). As Joel Thomas says: “Your initial decision locks one of the doors ... It’s not the door that opens, it’s the door you’re keeping closed that makes the difference.”

By opening door B, the host is effectively saying: “Between B and C, the only possibility is C.” We are given no new information about door A at all, only information about the relative probability between B and C, so A’s probability does not change.

So all of B’s water is poured into cup C, which now holds 2/3 litre. The contestant should change to door C, since it has the highest probability of having the car.

Digression: 100 doors

If you extended the Monty Hall problem to 100 doors instead of 3, with the host opening one door at a time to reveal goats behind all but one of them (other than the contestant’s door), then each cup of water for the opened doors gets evenly distributed between the cups of all the remaining closed doors except for the contestant’s one.

At the end (after 98 doors have been opened), the cup for the contestant’s door contains 1/100 litre, and the cup for the other remaining closed door contains 99/100 litre – the “concentrated probability” from all of the previously opened doors.

(Or think of it in terms of the card game analogy: Monty takes 99 cards then discards 98 non-Aces).

But even if only a single door was opened, the contestant would still be better off switching to any other door, since the amount of water in front of it would be greater than 1/100 litre (1/100 + 1/9800 = about 0.0101 litres).

(5) Two for the price of one

From user “Ted” on the Understanding the Monty Hall problem page:

Here’s another way to look at it: suppose after you pick one door, Monty offers to let you trade it for BOTH the other two doors ... Clearly you should should take the trade; your odds are twice as good with two doors. Well that’s the deal that Monty is offering in the problem except that he’s showing which of the other two doors has a goat (since at least one of them must have a goat behind it).

You’re essentially trading for both doors, but you know ahead of time what’s behind one of them. Whether he opens one of those two doors you traded for ahead of time or after the fact makes no difference – you should trade for the two doors to double your odds.

(6) To shift or not to shift

From user “Dinesh” on the Understanding the Monty Hall problem page:

There are three possible scenarios. Assume that out of A, B & C (A has car):

1. You pick A - you lose by shifting.
2. You pick B - you win by shifting.
3. You pick C - you win by shifting.

So you have 2 out of 3 chances of winning by shifting.

(7) Simulation

Perhaps the most direct way to explore the Monty Haul problem is to simulate it. There are plenty of simulators online, such as this one and one near the top of the understanding the Monty Hall problem page.

Alternatively, you can use three dice. If you happen to have some 3-sided dice (they do exist!), perfect. Otherwise use standard dice and subtract 3 when a value higher than 3 comes up (so 4 => 1, 5 => 2, 6 => 3).

Choose a strategy to use for the whole game (switch or stay), then do the following a large number of times:

• Roll one die to see which door the contestant picks (D1). (Or you can simplify things by assuming D1 is always 1).
• Roll another die to see where the car is (D2).
• If you are using the switch strategy, determine the “unopened door” D3 as follows:
• If D1 and D2 are different, D3 = D2. (The player has chosen a goat door, so the host must open the only other goat door, leaving the car door unopened).
• If D1 and D2 are the same, roll another die to find D3. If it comes up with the same value as D1 & D2, re-roll until it shows a different value. (The player has chosen the car door, so the unopened one is a random door with a goat).
• Score 1 point if:
• Your strategy is stay and D1 = D2.
• Your strategy is switch and D3 = D2. (If you think about it, this can only ever happen (and always happens) if D1 and D2 are different, so we don’t actually need to know D3. You could replace this rule with: “Your strategy is switch and D1 and D2 are different”).

The observant reader might notice something. When the strategy is stay, the problem reduces to: “If you roll two three sided dice, what is the probability that they are both the same number?” and the unopened door (D3) is irrelevant.

Which is another way of saying, the stay strategy succeeds 1/3 of the time, just as it would if the host never opened a door.

Probability and intuition

If the 2/3 result still feels wrong somehow, you are not alone. When Marilyn vos Savant (highest recorded IQ 1986-89 according to the Guinness Book of Records) responded to a question about the Monty Hall problem in a magazine in 1990, saying that the contestant should switch, she received thousands of letters claiming that her reasoning was flawed.

Harvard University Professor Persi Diaconis says there is no disgrace in getting this one wrong: “Our brains are just not wired to do probability problems very well.”

Here are some ways our intuition about probability can work against us.

All things being equal

People have a tendency to assign equal values to multiple unknown probabilities. Once one of the doors is opened, it feels automatic to assign the remaining doors a probability of 1/2 each. In other circumstances this might be correct, but more is going on in the Monty Hall problem than simply excluding an option.

A similar thing can happen when someone enumerates all the possibilities in a problem. If there are four basic outcomes, it feels natural to assign them a probability of 1/4 each. But this is not always justified, as seen in the decision tree for this problem.

Significance of changes

It can be easy to miss the significance of seemingly minor changes to a problem. The outcome is different if you change the set up of Monty Hall:

• If the host opens a goat door first then the contestant picks a door, the probability of it having the car is 1/2.
• If the host opens a door at random, and the game is declared void and restarted if he accidentally reveals the car (the Monty Fall problem described above), the probability becomes 1/2 as well .
• If two contestants play at the same time (in an attempt to create a contradiction where both players should switch), the host no longer has a choice of two doors to open, so it is not the same problem.

Information gained

The Monty Hall problem hinges on the fact that the host chooses between two doors to open, not all three. As explained under cups of water, no new information is gained about the contestant’s door when the goat door is revealed, so the probability associated with his door remains unchanged.

This is very easy to miss; choosing from two doors and opening one to reveal a goat looks a lot like choosing from three doors to reveal a goat. But the information gained in each case is different.

I think the most helpful analogy is a version of the card game with 100 cards. When Monty discards 98 non-Ace cards from his hand, he is only giving information about his own cards: if he has an Ace at all, it must be his last remaining card. If he revealed his cards at random, or he was allowed to reveal your card, then the probabilities would be different since the Ace would be involved. But since the Ace is guaranteed not to be revealed, there is no new information about whether you are holding it, so your probability remains at 1% for the whole game.

Not set in stone

Even when the correct answer is reached the reasoning can still be flawed. When explaining why the probability associated with the contestant’s door doesn’t change, some people use a statement like the following: “Once the player selects a door, the probability is set in stone.”

As Sasha Volkov writes: “Any explanation that says something like ‘The probability of door 1 was 1/3, and nothing can change that...’ is automatically fishy: probabilities are expressions of our ignorance about the world, and new information can change the extent of our ignorance.”

Probabilities can change, be redistributed or set to 0% or 100% as information gets updated. The tricky part is keeping track of exactly what we know at each stage.

Top – Maths – Home

Questions or comments to: [email protected]